基本原理介绍

基础定义

坐标系（Coordinate System）： 用一个原点和一组相互正交、带方向的基轴（常为 X、Y、Z）来定义的参考框架，用于在特定单位下唯一表示空间中点的位置与方向。

• 2D 含两轴（X、Y），3D 含三轴（X、Y、Z）；
• 需约定手性（常用右手系）与单位（mm、m 等）；
• 相对同一坐标系给出的向量和姿态具有可比性与可组合性。

常见坐标变换类型

平移（translation）: poseAdd()

• 含义：把同一个点在同一坐标系里挪位置，方向不变。
• 公式（点从B系表达变到A系时带平移）：

$${\mathbf{p}}_{\mathrm{A}}={\mathbf{R}}_{\mathrm{A}}^{\mathrm{B}}{\mathbf{p}}_{\mathrm{B}}+{\mathbf{t}}_{\mathrm{A}}^{\mathrm{B}}$$

这里 ${\mathbf{t}}_A^B=[t_x,t_y,t_z{]}^T$ 是 在A坐标系中 表达的平移向量。

• $\mathbf{R}$负责“转方向”，$\mathbf{t}$负责“加位置”。只有平移时就 ${\mathbf{p}}_A={\mathbf{p}}_B+\mathbf{t}$。

旋转（rotation）: poseRotation()

• 含义：在同一坐标系里转方向，位置相对原点绕圈改变。

• 公式：${\mathbf{p}}_A^{\prime }=\mathbf{R}{\mathbf{p}}_A$，$\mathbf{R}\in SO(3)$，满足 ${\mathbf{R}}^T\mathbf{R}=\mathbf{I}$，$det\mathbf{R}=+1$。

• 常用表示法（3D）：

  • 欧拉角 ZYX（yaw-pitch-roll）：$\mathbf{R}={\mathbf{R}}_z(\psi ){\mathbf{R}}_y(\theta ){\mathbf{R}}_x(\varphi )$
  • 轴—角（绕单位轴 $\hat{\omega }$ 旋转角 $\theta$）：罗德里格公式 $\mathbf{R}=\mathbf{I}+\sin \theta [\hat{\omega }{]}_{\times }+(1-\cos \theta )([\hat{\omega }{]}_{\times }{)}^2$

平移+旋转一起（位姿/齐次变换）: poseTrans()

把旋转和平移打包成一个 4×4：

$$\mathbf{T}=\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\\ {\mathbf{0}}^T& 1\end{array}\right],\left[\begin{array}{c}{\mathbf{p}}_A\\ 1\end{array}\right]={\mathbf{T}}_A^B\left[\begin{array}{c}{\mathbf{p}}_B\\ 1\end{array}\right]$$

• 组合顺序：右乘离点更近的那个变换。 例如先在TCP自身系里偏移/旋转（$\mathrm{\Delta }{\mathbf{T}}_{tcp}$），再放回基座：

$${\mathbf{T}}_{\mathrm{base}}^{\mathrm{tcp},\mathrm{new}}={\mathbf{T}}_{\mathrm{base}}^{\mathrm{tcp}}\mathrm{\Delta }{\mathbf{T}}_{\mathrm{tcp}}$$

• 逆变换 poseInverse()： 把“从 B 到 A 的位姿”转换到“从 A 到 B 的位姿”,

$${\mathbf{T}}^{-1}=\left(\begin{array}{cc}{\mathbf{R}}^{\mathsf{T}}& -{\mathbf{R}}^{\mathsf{T}}\mathbf{t}\\ \mathbf{0}& 1\end{array}\right)$$

应用示例

1. 点位偏移

示例程序包

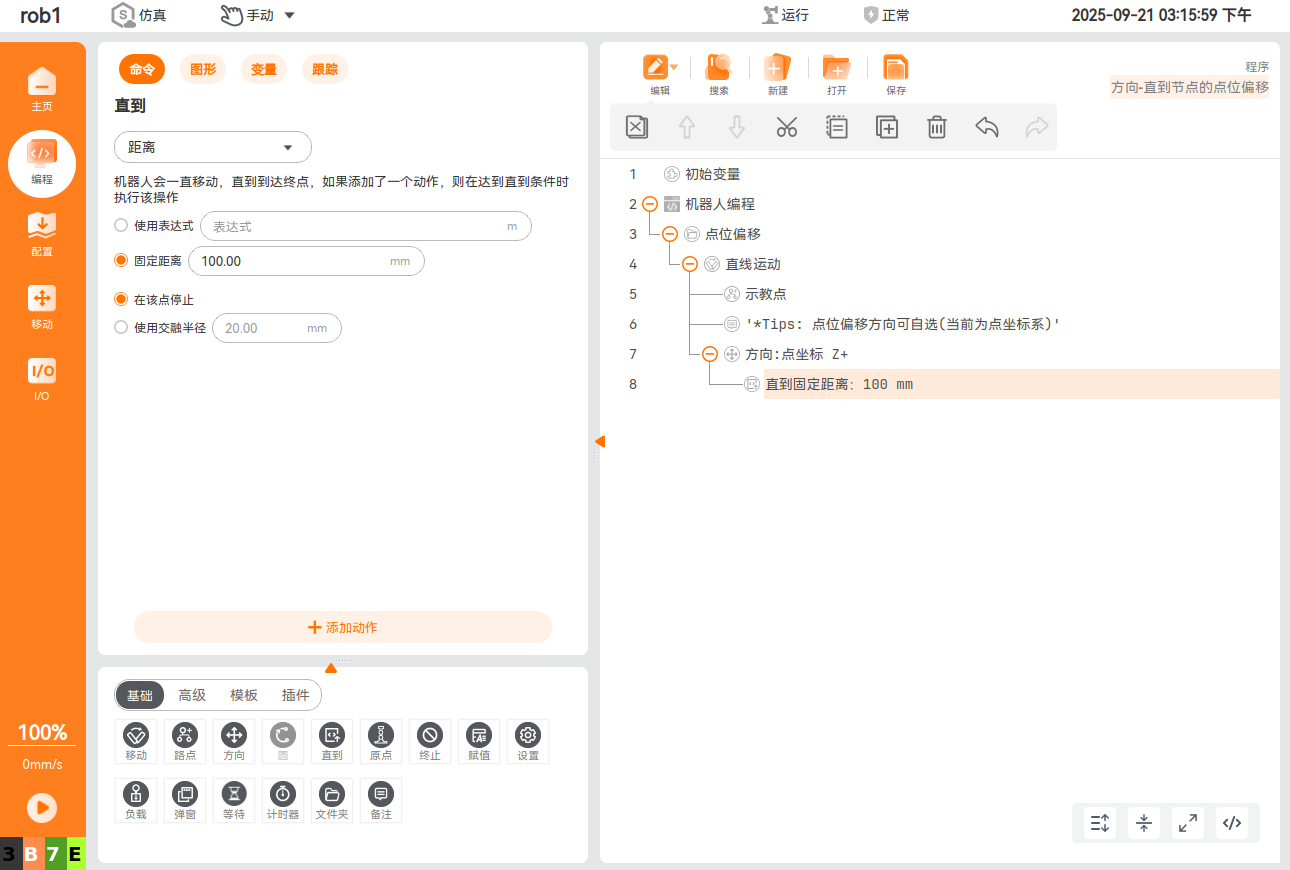
1. 方向-直到节点实现点位偏移

   

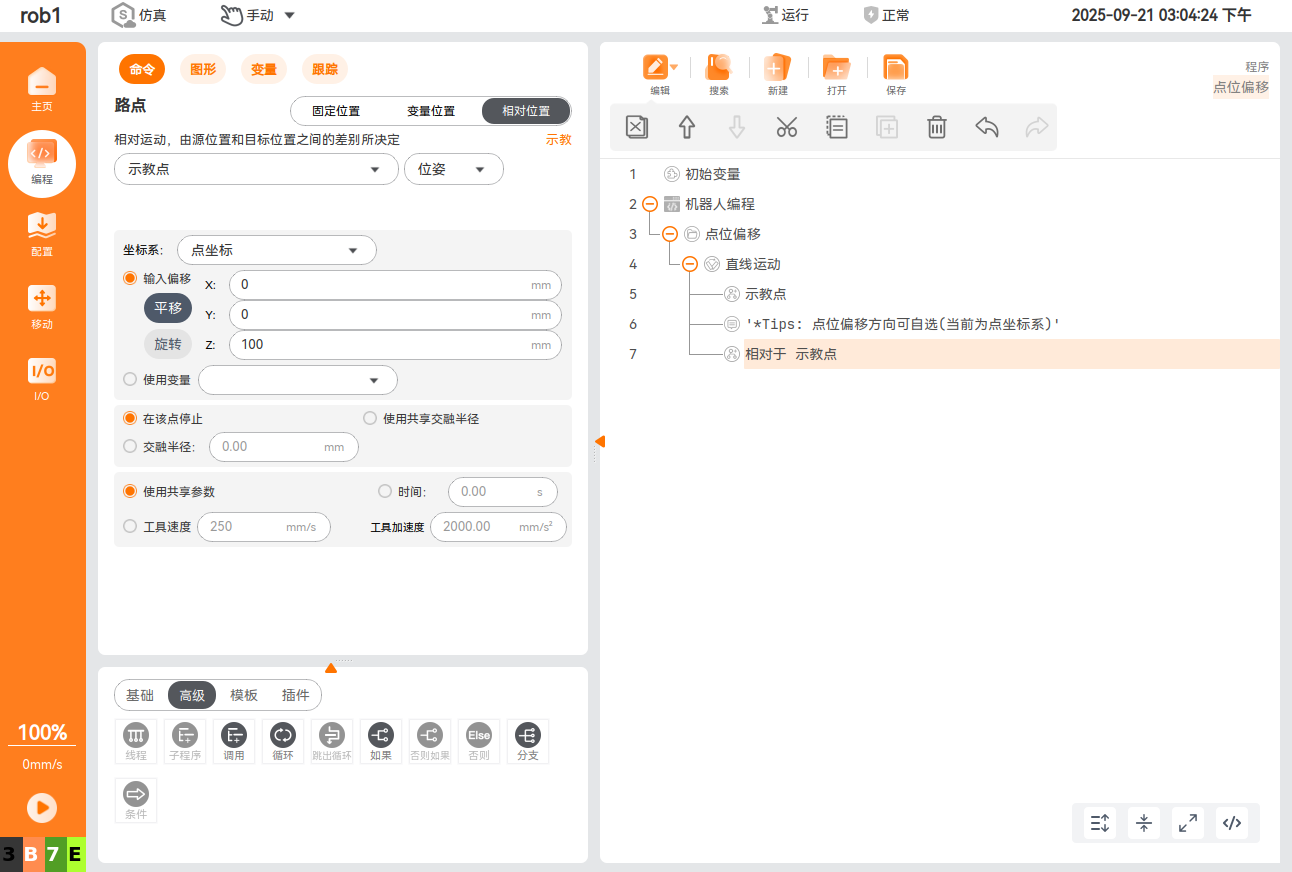
2. 0.31分支特性：相对于变量或路点实现点位偏移

   

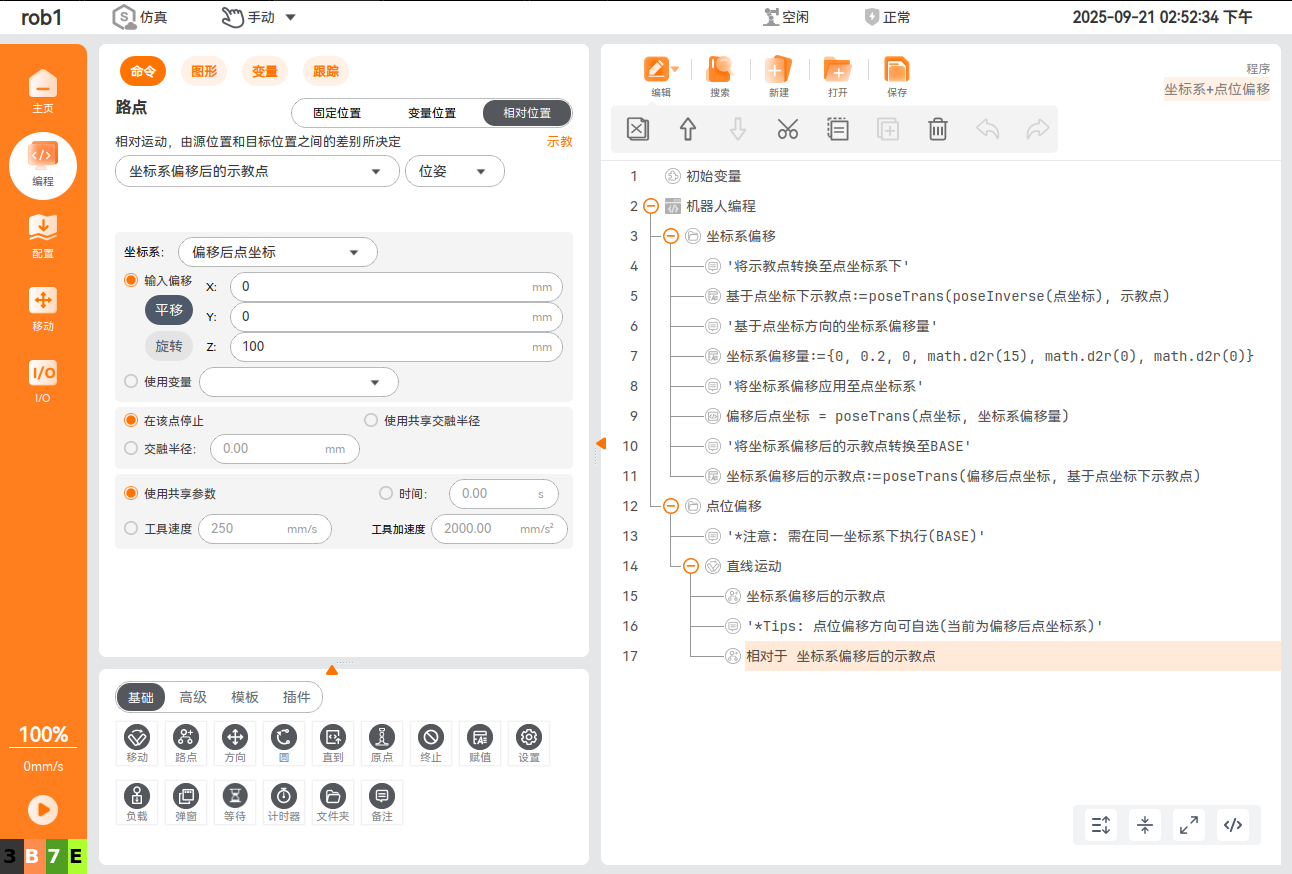
2. 坐标系偏移

1. 通过自定义坐标系实现偏移

   

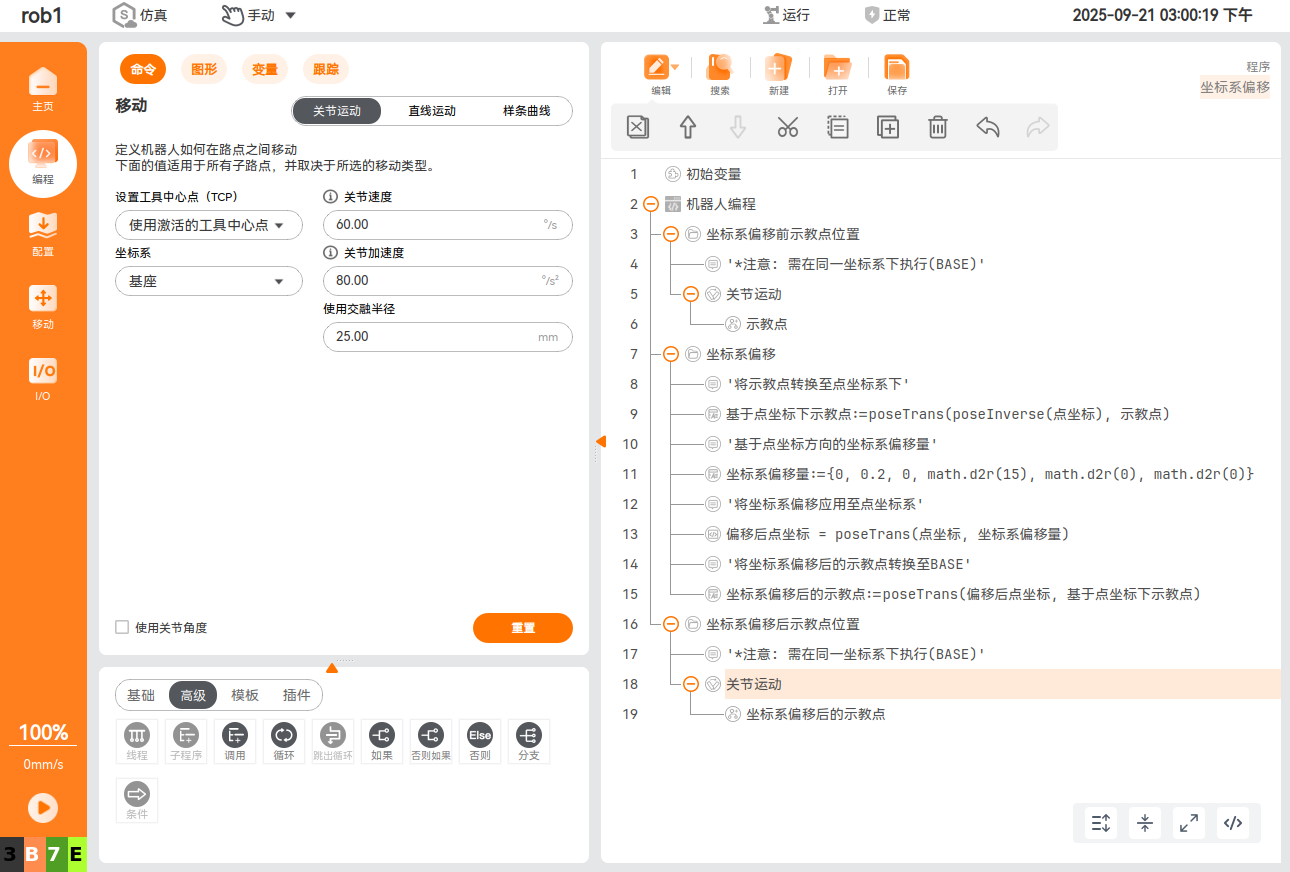
2. 坐标系 + 点位偏移